True/False
Indicate whether the
statement is true or false.
|
|
|
1.
|
An angle in standard position has an initial arm located on the
x-axis.
|
|
|
2.
|
Exactly three angles between 0° and 360° have the same value for the
sine ratio.
|
|
|
3.
|
The CAST rule identifies positive primary trigonometric ratios for
angles.
|
|
|
4.
|
The reciprocal trigonometric ratios are cosecant, secant, and cotangent.
|
|
|
5.
|
When two solutions exist for given information in a trigonometry problem, it is
referred to as the arbitrary case.
|
|
|
6.
|
Solving a problem in three dimensions usually involves solving two problems that
are each two-dimensional problems.
|
|
|
7.
|
The expression 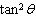 can also be written as 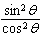 .
|
Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
8.
|
For the given triangle, tan A is equal to which expression? 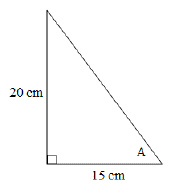
|
|
|
9.
|
Which statement regarding sin 30° is true?
a. | sin 30° = cos 60° | c. | sin 30° = sin
150° | b. | sin 30° = 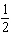 | d. | all of the
above |
|
|
|
10.
|
What is the measure of ÐB in the triangle
shown? 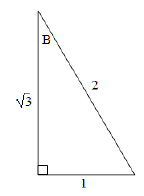
|
|
|
11.
|
What reference angle should be used for an angle of 300° in standard
position?
|
|
|
12.
|
In which quadrants are the tangent ratios negative values?
a. | first and second | c. | third and fourth | b. | second and third | d. | second and
fourth |
|
|
|
13.
|
Which set of angles has the same terminal arm as 40°?
a. | 400°, 760°, 1120° | c. | 130°, 220°,
310° | b. | 220°, 400°, 580° | d. | 80°, 120°,
200° |
|
|
|
14.
|
The point (3, 4) is on the terminal arm of ÐA.Which is the set of exact primary trigonometric ratios for the
angle?
|
|
|
15.
|
The point (3, –5) is on the terminal arm of ÐD.Which is the set of exact primary trigonometric ratios for the
angle?
|
|
|
16.
|
What is the exact value for 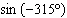 ?
|
|
|
17.
|
Which pair of angles between 0° and 360° satisfies 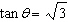 ? a. | –60° and –240° | c. | 120° and
240° | b. | 60° and 240° | d. | 300° and 240° |
|
|
|
18.
|
What is the measure of ÐA, if 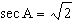 and
ÐA is located in the first quadrant? a. | 70.5° | c. | 22.5° | b. | 45° | d. | 135° |
|
|
|
19.
|
Which of the following is the correct expression for csc A?
|
|
|
20.
|
Determine two angles between 0° and 360° that have a cosecant of
–2.
a. | 30° and 150° | c. | 330° and 210° | b. | –30° and
–150° | d. | 240°
and 300° |
|
|
|
21.
|
In solving a triangle, which of the following situations requires the ambiguous
case to be considered?
a. | two sides and one opposite angle | c. | three sides | b. | two sides and the
contained angle | d. | one side
and two angles |
|
|
|
22.
|
Which strategy would be best to solve for x in the triangle
shown? 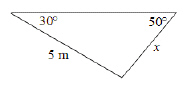 a. | sine law | c. | primary trigonometric ratio | b. | cosine
law | d. | none of the
above |
|
|
|
23.
|
Determine the length of x, to the nearest tenth of a metre. 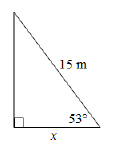 a. | 24.9 m | c. | 12.0 m | b. | 9.0 m | d. | 18.8 m |
|
|
|
24.
|
Determine the length of x, to the nearest tenth of a centimetre. 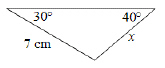 a. | 5.4 cm | c. | 9.0 cm | b. | 7.9 cm | d. | 6.2 cm |
|
|
|
25.
|
Determine the length of x, to the nearest tenth of a metre. 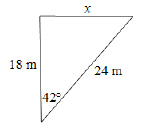 a. | 257.9 m | c. | 15.9 m | b. | 39.3 m | d. | 16.1 m |
|
|
|
26.
|
Determine the measure of x, to the nearest tenth of a degree. 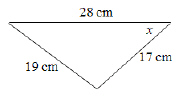 a. | 48.4° | c. | 20.8° | b. | 41.6° | d. | 35.5° |
|
|
|
27.
|
Determine the length of x, to the nearest tenth of a kilometre. 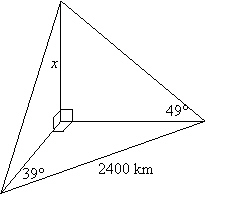 a. | 2100.0 km | c. | 2400.0 km | b. | 1737.5 km | d. | 990.9 km |
|
|
|
28.
|
What does the expression 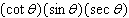 simplify to?
|