Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
If x3 – 4x2 + 5x – 6 is
divided by x – 1, then the restriction on x is
a. | x 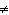 –4 –4 | c. | x 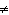 1
1 | b. | x 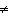 –1 –1 | d. | no restrictions |
|
|
|
2.
|
What is the remainder when x4 + 2x2 –
3x + 7 is divided by x + 2?
|
|
|
3.
|
If 2x3 – 9x2 + 4x – 7 is
divided by x – 3 to give a quotient of 2x2 – 3x – 5
and
a remainder of –22 , then which of the following is true?
a. | 2x3 – 9x2 + 4x – 7 =
(x – 3)(2x2 – 3x – 5) + 22 | b. | 2x3 – 9x2 + 4x – 7 =
(x – 3)(2x2 – 3x – 5) –
22 | c. | (x – 3)(2x2 – 3x – 5) =
22 | d. | (x – 3)(2x2 – 3x – 5) =
–22 |
|
Short Answer
|
|
|
4.
|
Complete this question and bring to class.
a) Use long division to
divide x3 + 3x2 – 7 by x + 2. Express the result in
quotient form.
b) Identify any restrictions on the variable.
c) Write the
corresponding statement that can be used to check the division.
d) Verify your
answer.
|